It’s a fine day for the Universe to die, and to be new again! Well, maybe not, but the Internet is abuzz with a reincarnation of the unstable universe story. (You can also see it here, or here, the whole thing is trending in Google). In other works, this is known as tunneling between vacua. And if you have followed the news about the Landscape of vacua in string theory, this should be old news (that we may live in a unstable Universe, which we don’t know). For some reason, this wheel gets reinvented again and again with different names. All you need is one paper, or conference, or talk to make it sound exciting, and then it’s “Coming attraction: the end of the Universe …. a couple of billion years in the future“.
The basic idea is very similar to superheated water, and the formation of water bubbles in the hot water. What you have to imagine is that you are in a situation where you have a first order phase transition between two phases. Call them phase A and B for lack of a better word (superheated water and water vapor), and you have to assume that the energy density in phase A is larger than the energy density in phase B, and that you happened to get a big chunk of material in the phase A. This can be done in some microwave ovens and you can have water explosions if you don’t watch out.
Now let us assume that someone happened to nucleate a small (spherical) bubble of phase B inside phase A, and that you want to estimate the energy of the new configuration. You can make the approximation that the wall separating the two phases is thin for simplicity, and that there is an associated wall (surface) tension  to account for any energy that you need to use to transition between the phases. The energy difference (or difference between free energies) of the configuration with the bubble and the one without the bubble is
to account for any energy that you need to use to transition between the phases. The energy difference (or difference between free energies) of the configuration with the bubble and the one without the bubble is
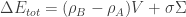
Where  are the energy densities of phase A, phase B,
are the energy densities of phase A, phase B,  is the volume of region B, and
is the volume of region B, and 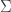 is the surface area between the two phases.
is the surface area between the two phases.
If  , then the surface term has more energy stored in it than the volume term. In the limit where we shrink the bubble to zero size, we get no energy difference. For big volumes, the volume term wins over the area, and we get a net lowering of the energy, so the system would not have enough energy in it to restore the region filled with phase B with phase A. In between there is a Goldilocks bubble that has the exact same energy of the initial configuration.
, then the surface term has more energy stored in it than the volume term. In the limit where we shrink the bubble to zero size, we get no energy difference. For big volumes, the volume term wins over the area, and we get a net lowering of the energy, so the system would not have enough energy in it to restore the region filled with phase B with phase A. In between there is a Goldilocks bubble that has the exact same energy of the initial configuration.
So if we look carefully, there is an energy barrier between being able to nucleate a large enough Goldilocks bubble so that there is no net change in energy from a situation with no bubble. If the bubbles are too small, they tend to shrink, and if the bubbles are big they start to grow even bigger.
There are two standard ways to get past such an energy barrier. In the first way, we use thermal fluctuations. In the second one (the more fun one, since it can happen even at zero temperature), we use quantum tunneling to get from no bubble, to bubble. Once we have the bubble it expands.
Now, you might ask, what does this have to do with the Universe dying?
Well, imagine the whole Universe is filled with phase A, but there is a phase B lurking around with less energy density. If a bubble of phase B happens to nucleate, then such a bubble will expand (usually it will accelerate very quickly to reach the maximum speed in the universe: the speed if light) and get bigger as time goes by eating everything in its way (including us). The Universe filled with phase A gets eaten up by a universe with phase B. We call that the end of the Universe A.
You need to add a little bit more information to make this story somewhat consistent with (classical) gravity, but not too much. This was done by Coleman and De Luccia, way back in 1987. You can find some information about this history here. Incidentally, this has been used to describe how inflating universes might be nucleated from nothing, and people who study the Landscape of string vacua have been trying to understand how this tunneling between vacua might seed the Universe we see in some form or another from a process where these tunneling events explore all possibilities.
You can reincarnate that into Today’s version of “The end is near, but not too near”. We know the end is not too near, because if it was, it would have already happened. I’m going to skip this statistical estimate: all you have to understand is that the expected time that it would take to statistically nucleate that bubble somewhere has to be at least the age of the currently known universe (give or take). I think the only reason this got any traction was because the Higgs potential in just the Standard model, with no dark matter, with no nothing more in all its possible incarnations is involved in it somehow.
Next week: see baby Universe being born! Isn’t it cute? That’s the last thing you’ll ever see: Now you die!
Fine print: Ab initio calculations of the “vacuum energies” and “tunneling rates” between various phases are not model independent. It could be that the age of the current Universe is in the trillions or quadrillions of years if a few details are changed. And all of these details depend on the physics at energy scales much larger than the standard model, the precise details of which we don’t know much at all. The main reason these numbers can change so much is because a tunneling rate is calculated by taking the exponential of a negative number. Order one changes in the quantity we exponentiate lead to huge changes in estimates for lifetimes.
Read Full Post »
